巻取理論はロール品質の客観的な評価や最良な巻取条件の見極めに有益である。ここでは巻取理論で最も有名なHakielモデルについて紹介する。
Hakielモデルの概要と仮定
Hakielモデルが今日における巻取理論の基礎
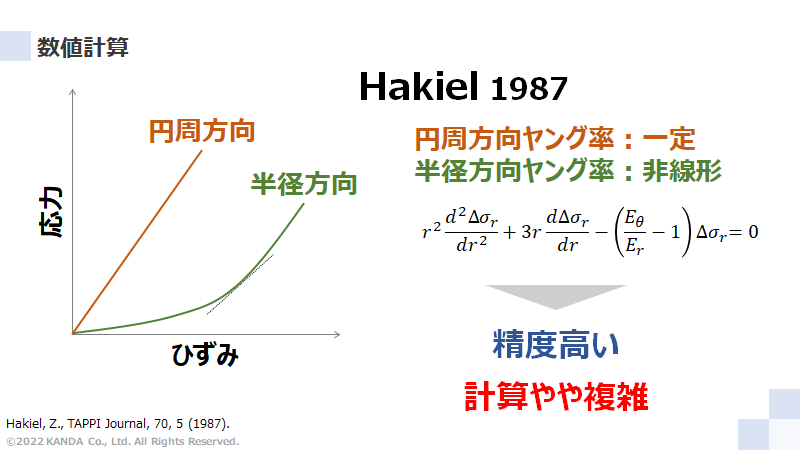
Hakiel氏が半径方向ヤング率の非線形性を考慮した理論モデルを1987年に発表した。これにより、以前のモデルと比較して巻取ロールの内部応力の予測精度がかなり向上した。その後の1990年代にはHakielモデルを基礎とし、さまざまな影響を考慮した修正モデルが順次発表されてきた。
Hakielモデルの価値は、さまざまな現象を考慮できる汎用性の高さにある。これは巻取工程を理論的に取り扱うために設定した次の仮定による。
- 巻取ロールは完全な円筒形状を保ち、ロール内においてウェブの厚さ、幅、表面粗さなどは均一であり、変化しない。
- ウェブはスパイラル状ではなく、引っ張られた薄肉円筒の積み重ねで表現する。また、単一の薄肉円筒における弾性特性は一定とする。
- 巻取ロールは直交異方性の弾性体とし、円周方向は線形、半径方向は非線形のヤング率をそれぞれ仮定する。
簡単にいえば(1)巻取工程における不安定要素を排除して理想化し、(2)巻き取る操作を計算しやすいように表現し、(3)ウェブ表面の粗さに起因した半径方向ヤング率の非線形性を考慮している。
ウェブのヤング率の評価とその事例
理論モデルに適用するウェブのヤング率は引張試験と圧縮試験で評価
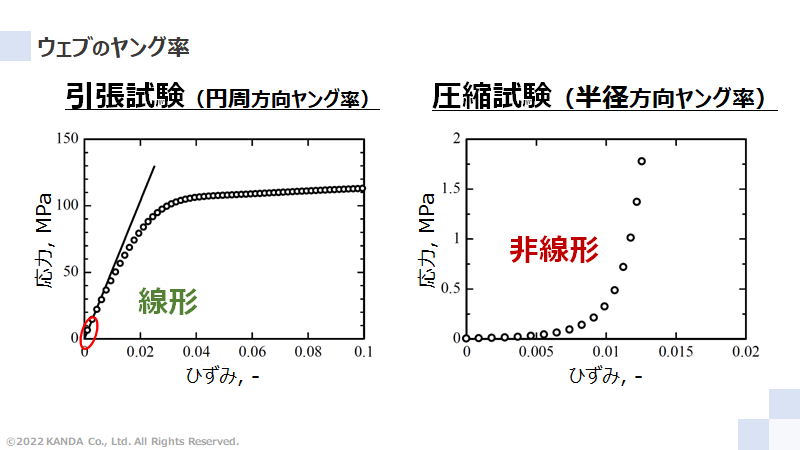
あるプラスチックフィルムのヤング率を評価した引張試験と圧縮試験のデータである応力‐ひずみ線図をそれぞれ左図と右図に示している。引張試験データから円周方向ヤング率(巻取方向のヤング率)、圧縮試験データから半径方向ヤング率(厚み方向のヤング率)をそれぞれ数値化する。
数値化には巻取ロール内の応力範囲を念頭に置く必要がある。多くの場合で巻取ロールの内部応力は、引張試験の線形範囲、圧縮試験の非線形範囲である。したがって、円周方向ヤング率を一定値、半径方向ヤング率を応力に依存した近似式として理論モデルに適用する。
内部応力の数値計算イメージ
ウェブの巻取りを薄肉円筒の積み重ねで表現した数値計算
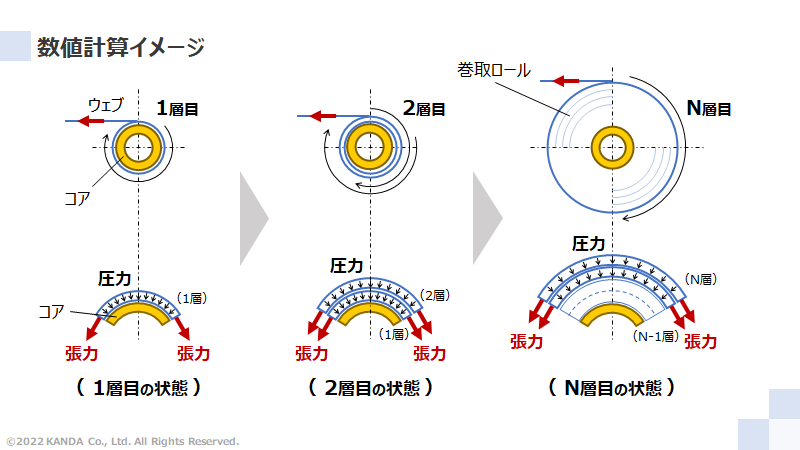
巻取り始めの1層目は張力によって引っ張られたウェブがコアに巻かれる。このときコアには張力に起因した圧力(=張力/ロール半径)が負荷される。さらに2層目に巻かれると、コアと1層目のそれぞれに2層目を巻いたことによる圧力が負荷される。このようにしてウェブが次々と巻き取られ、N層目が巻かれた時にはコア、1層目、2層目・・・(N-1)層目に対してN層目を巻いたことによる圧力が負荷される。このように巻取ロールの内部応力は最外層に巻いたウェブがその内層側の各層に作用する圧力を順次加算して計算していく。
なお、最外層を巻くことによる圧力の影響力は内層側ほど小さくなる。内部応力は単純な足し算では求められないことに注意が必要である。
Hakielモデルでの数値計算の例
巻取り中の内部応力の変動を数値計算した事例を紹介
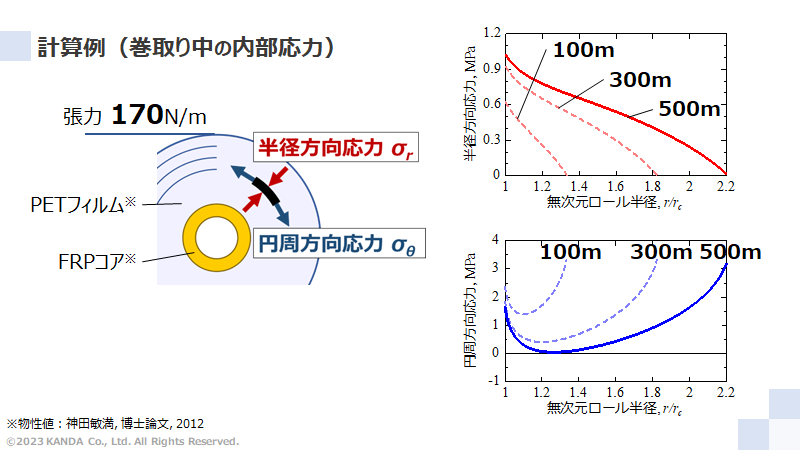
あるPETフィルムを巻取張力170N/mで500m巻くことを想定した。半径方向応力と円周方向応力の数値計算結果には巻取途中の100mと300m、最後の500mにおける値をそれぞれ示している。なお、横軸の無次元ロール半径は巻取ロール径をコア径で除したものであり、1がコア位置、2.2が最外層の500m位置である。
半径方向応力の結果から、いずれの巻取長でも最内層が最も大きな値であり、最外層に向かって減少していることがわかる。これはウェブを次々と巻き取ることでその内層側の各層に圧力が作用した結果である。また、100m、300m、500mと巻取りが進むと全体的に半径方向応力が増大していくが、内層側ほど増大量は小さい。これは最外層を巻くことによる圧力の影響力は内層側ほど小さくなることによる。
一方、円周方向応力はいずれの巻取長でも凹形状になっている。すでに巻き取られた内層側のウェブは、巻かれた時点よりも円周方向に圧縮されていくことわかる。
内部応力の数値計算の利点
巻取トラブルの原因探索と最良な巻取条件の決定に有益
巻取ロールの内部応力を数値化することで、内部応力と相関する巻取トラブルの根本原因を究明しやすくなる。また、さまざまな巻取条件での内部応力を定量比較できるため、トラブルが発生しにくい巻取条件の決定にも役立つ。
これには数値化された内部応力と巻取トラブルの関係性を読み解くスキルを磨くことが重要なポイントになる。
関連ページ
 ウェブハンドリング
ウェブハンドリング